二叉树的各种遍历
最近在刷牛客网的题,刷到一个二叉树的题。记得有一次别人问我让我写一个简单的二叉树遍历,广度优先,深度优先的。。我说不太会,对方就说leetcode上基本一半的题都是这种BFS和DFS的。。当时根本没有涉及过这一块,觉得自己太菜。今天既然刷到这道题,就把这一块都好好总结一下。
这是基本的树结构,先定义这么一个类。
function TreeNode(value) { this.value = value; this.left = null; this.right = null;}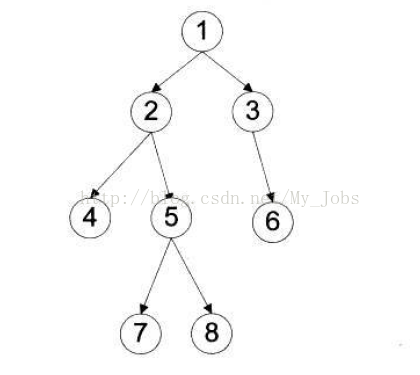
前序排列: 1 2 4 5 7 8 3 6
中序排列: 4 2 7 5 8 1 3 6
后序排列: 4 7 8 5 2 6 3 1
前序排列#
前序排列是按照 根节点->左节点->右节点的顺序,来遍历整个二叉树。
先使用递归的方法来写前序遍历,每到一个非空的节点,就对当前节点的值进行操作,然后找左节点的值,当左节点走到尽头时,该函数就结束,接着找右节点。
//递归的方法写前序遍历,根节点->左节点->右节点var preOrderTraverse = function(root) { if(root!=null) { console.log(root.value); //直接在这里对值进行操作 preOrderTraverse(root.left); preOrderTraverse(root.right); }}用栈的方式写前序排列,需要维护一个栈,将每个可能分叉的树节点都push到栈里,然后一直遍历左侧子节点。当走不下去的时候,就返回上一步,找到上一个节点的右节点,把值取出来,但下一步还是找这个新的节点的左节点,直到走到尽头。
//用栈来写前序遍历var preOrderTraverse1 = function(root) {
let pNode = root; let stack = []; while(pNode!=null || stack.length) { if(pNode!=null) { console.log(pNode.value); stack.push(pNode); pNode = pNode.left; } else { let temp = stack.pop(); pNode = temp.right; } }}中序遍历和前序遍历不一样的地方是顺序,左节点->根节点->右节点。
在写递归的时候,可以发现与前序遍历唯一不一样的地方就是调用值的顺序不同。是在最左侧的树到了尽头之后,再对值进行操作。所以这是一个典型的深度优先搜索。
//递归的方法写中序遍历,左节点->根节点->右节点var inOrderTraverse = function(root) { if(root!=null) { inOrderTraverse(root.left); console.log(root.value); inOrderTraverse(root.right); }}
//用栈的方法写中序排序,左节点->根节点->右节点var inOrderTraverse1 = function(root) { let pNode = root; let stack = []; while(pNode!=null || stack.length) { if(pNode!=null) { stack.push(pNode); pNode = pNode.left; //走到宇宙的尽头,当然是左尽头 } else { pNode = arr.pop(); //将“当前”尽头的节点弹出栈 console.log(pNode.value); pNode = pNode.right; } }}后序遍历与之前的区别,就是取值是在遍历完左右节点之后。
//递归的方法写后序遍历,左节点->右节点->根节点var postOrderTraverse = function(root) { if(root!=null) { postOrderTraverse(root.left); postOrderTraverse(root.right); console.log(root.value); }}广度优先需要维护一个队列,先进先出。每次遇到一个非空值,就把当前值取出来。然后依次查看左右子节点是否非空,非空就从队尾加入队列。
//层次遍历二叉树——广度优先搜索的实现var levelTraverse = function(root) { let arr = []; //这是个队列 arr.push(root);
while(arr.length) { let pNode = arr.shift(); //是队列,先进先出,所以从头部取出来 console.log(pNode.value); //将当前的值使用 if(pNode.left!=null) arr.push(pNode.left); // if(pNode.right!=null) arr.push(pNode.right); }}